
Statistical Design of Experiments
Statistical Design of Experiments
Statistical Design of Experiments
Statistical Design of Experiments
The Formulas:
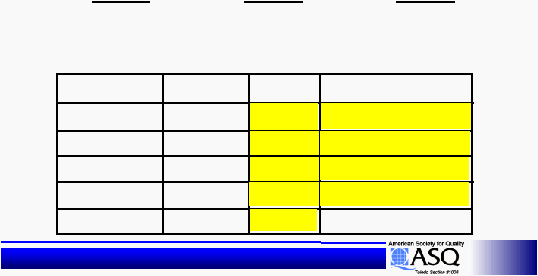
Two -Way ANOVA
Two -Way ANOVA
Total SS =
Total SS =
Observations
Total
ObservationTotal of all Observations)SS(E)
each
rab
2
2
2
2
Source
d.f.
SS
MS ~ Variance
Error
TOTAL
Factor B
Factor A
Interaction (AB)
(a -
1)
(b -
1)
(a -1) (b -1)
(n -
ab)
(n -
1)
SS(A)
SS(B)
SS(AB)
SSE
Total SS
SS(A) / (a -
1)
SS(B) / (b -
1)
SS(AB) / (a -
1)(b -
1)
SSE / (n -
ab)
Total SS
n = rabSS(A)
= total number of observations
r = number of times each factorial treatment
combination appears in the experiment
(replication)
SS(A) =
SS(A) =
(Each level total of A)²
(Each level total of A)²
2
rb
rb
-
-
(Total of all Observations)²
(Total of all Observations)²
2
rab
rab
SS(A)
SS(B)
SS(B) =
SS(B) =
(Each level total of B)²
(Each level total of B)²
2
ra
ra
-
-
(Total of all Observations)²
(Total of all Observations)²
2
rab
rab
SS(AB)
SS(AB) =
SS(AB) =
(Each Treat. Comb. Total)
(Each Treat. Comb. Total)
2
2
r
r
-
-
(Total of all Observations)
(Total of all Observations)SS(E)
2
2
rab
rab
-
-
SSA-
SSA-
-
SSB
SSB
SS
SS
Error
Error
= Total SS -
= Total SS -
SSA -
SSA -
SSB -
SSB -
SS(AB)
SS(AB)
SSE
SS(A) / (a -
1)
MS(B) =
MS(B) =
SS(B)
SS(B)
d.f.(B)
d.f.(B)
SS(B) / (b -
1)
MS(AB) =
MS(AB) =
SS(AB)
SS(AB)
d.f.(AB)
d.f.(AB)
SS(AB) / (a -
1)(b -
1)
MSE =
MSE =
SS(E)
d.f.(E)
d.f.(E)
SSE / (n -
ab)
MS(A) =
MS(A) =
SS(A)
d.f.(A)
d.f.(A)
To test EACH null hypothesis: Calculate the F
statistic for each factor or interaction and compare
against the Critical value of F to determine if it
significantly affects the response variable
F =
F =
MS(A)
MS(A)
MSE
MSE
F =
F =
MS(B)
MS(B)
MSE
MSE
F =
F =
MS(AB)
MS(AB)
MSE
MSE