Full Factorial Design: Comprehensive Guide for Optimal Experimentation

The full factorial design distinguishes itself as a robust, enlightening experimentation approach across industries.

At its core, this systematic method examines multiple metrics’ collective effects on an outcome simultaneously.

Considering all factor level combinations furnishes holistic comprehension beyond individual impacts—illuminating intricate relationships shaping complex systems’ behaviors.

The factorial design’s strength lies in realistically emulating dynamics’ nuances where variables interact intricately nonlinearly. Accounting for interplays guards against oversimplification. This casts light on underlying realities profoundly, priming informed resolutions and refinement pursuits.

From manufacturing to research frontiers, ponder occasions where exhaustively investigating factor relations meaningfully addresses specific problems or opportunities.

Key Highlights

• A comprehensive exploration of factor effects and interactions
• Robust methodology for process understanding and optimization
• Applications across diverse industries, including manufacturing, pharmaceuticals, and marketing
• Rigorous statistical analysis techniques, such as ANOVA and regression modeling
• Insights into factor-level optimization for enhanced process performance
• Evaluation of alternative designs, including fractional factorial and response surface methodologies
• Best practices for experimental design, data collection, and analysis

Introduction to Full Factorial Design

The full factorial design stands out as a comprehensive and robust approach, enabling researchers and practitioners to unlock valuable insights and drive meaningful change across diverse industries.

The full factorial design is a systematic way to investigate the effects of multiple factors on a response variable simultaneously.

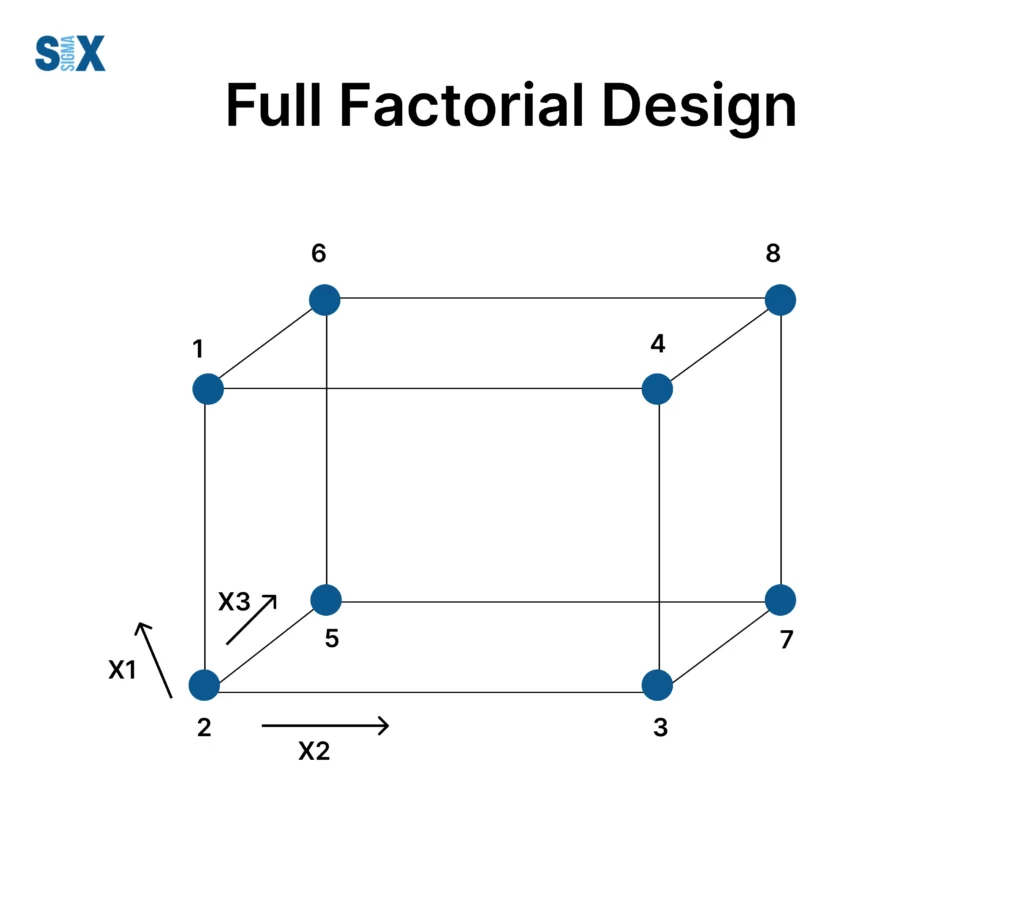
By considering all possible combinations of factor levels, this experimental strategy provides a holistic understanding of not only the individual factor effects but also the intricate interactions that can shape outcomes in complex systems.

A full factorial design is an experimental design that considers the effects of multiple factors simultaneously on a response variable.

It involves manipulating all possible combinations of the levels of each factor, enabling researchers to determine the main effects of individual factors as well as their interactions statistically.

This comprehensive approach ensures that no potential interaction is overlooked, providing a complete picture of the system under investigation.

The key benefits of employing a full factorial design include:

• Main effects: Researchers can identify which factors have the most significant impact on the response variable, allowing them to focus their efforts on the most influential factors.
• Interaction effects: By accounting for interactions between factors, full factorial designs reveal how the effect of one factor depends on the level of another factor, providing insights into the complex relationships within the system.
• Optimization: With a comprehensive understanding of the main effects and interactions, researchers can estimate the optimal settings for the independent variables, leading to the best possible outcome for the response variable.

The versatility of the full factorial design makes it a valuable tool across various industries, including:

• Manufacturing: Optimizing processes, improving product quality, and reducing defects by identifying key variables and their interactions.
• Pharmaceuticals: Formulating and developing drugs by assessing factors such as excipient concentrations, drug particle size, and processing conditions on bioavailability, stability, and release profiles.
• Marketing: Optimizing promotional strategies by evaluating the effects of factors like ad content, media channels, target audience segments, and pricing on consumer response.

Fundamentals of Design of Experiments (DOE)

Before delving into the intricacies of full factorial design, it is essential to understand the fundamental principles of Design of Experiments (DOE), a systematic approach to investigating the relationships between input variables (factors) and output variables (responses).

DOE provides a structured framework for planning, executing, and analyzing experiments, ensuring reliable and insightful results.

Understanding Factors and Levels

In a DOE study, the variables that are manipulated or controlled by the experimenter are known as independent variables or factors.

These can be further classified into:

• Numerical factors: Variables that can take on a range of numerical values, such as temperature, pressure, or time.
• Categorical factors: Variables that have distinct, non-numerical levels, such as material type or production method.

The outcome or characteristic of interest that is measured and analyzed in an experiment is referred to as the response variable or dependent variable.

Common examples include product yield, strength, purity, or customer satisfaction.

Each independent variable in a DOE study can be set at different levels or values.

The choice of factor levels is crucial, as it determines the range of conditions under which the experiment is conducted.

Carefully selecting factor levels ensures that the study captures the relevant region of interest and provides meaningful insights into the system’s behavior.

Principles of DOE

Replication refers to the practice of repeating the same experimental run multiple times under identical conditions.

This allows researchers to estimate the inherent variability in the experimental process and ensures the reliability of the results by providing a measure of experimental error.

Randomization is the process of randomly assigning experimental runs to different factor level combinations.

This helps to mitigate the potential impact of nuisance variables and ensures that any observed effects can be attributed to the factors under investigation, rather than uncontrolled sources of variation.

Blocking is a technique used to account for known sources of variability in an experiment, such as differences in equipment, operators, or environmental conditions.

By grouping experimental runs into homogeneous blocks, researchers can isolate and quantify the effects of these nuisance variables, ensuring more precise estimates of the factor effects.

Types of Full Factorial Designs

Full factorial designs can be classified into different types based on the number of levels for each factor and the nature of the factors themselves.

Understanding the various types of full factorial designs is crucial for selecting the appropriate experimental strategy to address specific research questions or process optimization objectives.

2-Level Full Factorial Design

The 2-level full factorial design, where each factor has two levels (typically labeled as “low” and “high”), is commonly employed in screening experiments.

These experiments aim to identify the most significant factors influencing the response variable, allowing researchers to focus their efforts on the most promising factors in subsequent, more in-depth investigations.

By evaluating the main effects and interactions in a 2-level full factorial design, researchers can determine which factors have a statistically significant impact on the response variable.

This information is invaluable in prioritizing factors for further optimization or confirming their negligible influence, thereby streamlining the overall experimental process.

3-Level Full Factorial Design

Unlike the 2-level design, which assumes a linear relationship between factors and the response variable, the 3-level full factorial design allows for the investigation of quadratic effects.

These nonlinear effects can be important in scenarios where the response variable exhibits curvature or a peak/valley behavior within the explored factor ranges.

By incorporating three levels for each factor, researchers can model the curvature in the response surface more accurately.

This enhanced understanding of the system’s behavior enables more precise optimization and provides insights into potential optimal operating regions or factor level combinations.

Mixed-Level Full Factorial Design

In many real-world applications, experiments may involve a combination of categorical factors (e.g., material type, production method) and continuous factors (e.g., temperature, pressure).

The mixed-level full factorial design accommodates this scenario by allowing researchers to investigate the effects of both types of factors simultaneously, providing a comprehensive understanding of the system.

Analyzing Full Factorial Design Experiments

Once the experimental data has been collected, the next step is to analyze the results to gain insights into the main effects, interactions, and optimal factor level combinations.

Several statistical techniques are employed in the analysis of full factorial experiments, each serving a specific purpose and providing valuable information for process understanding and optimization.

Analysis of Variance (ANOVA)

Analysis of Variance (ANOVA) is a powerful statistical tool used to determine the significance of main effects (individual factor effects) and interaction effects (combined effects of multiple factors) on the response variable.

By partitioning the total variability in the data into components attributable to each factor and their interactions, ANOVA enables researchers to identify the most influential factors and their relationships.

ANOVA also provides a framework for hypothesis testing, allowing researchers to assess whether the observed effects are statistically significant or simply due to random variability.

This rigorous approach ensures that conclusions drawn from the experimental data are statistically valid and reliable.

Regression Analysis

Regression analysis is another essential tool in the analysis of full factorial experiments.

It involves fitting a mathematical model to the experimental data, relating the response variable to the independent variables (factors) and their interactions.

This model can be used to predict the response variable for any combination of factor levels within the experimental region.

Once a suitable regression model has been obtained, researchers can employ optimization techniques to identify the factor level combinations that maximize or minimize the response variable.

These techniques often involve solving the regression equation subject to relevant constraints, enabling the determination of optimal operating conditions for the process under investigation.

Graphical Analysis & Full Factorial Design

Graphical analysis is a powerful tool for visualizing and interpreting the results of full factorial experiments.

Interaction plots are particularly useful for examining the presence and nature of interactions between factors.

These plots display the response variable as a function of one factor at different levels of another factor, allowing researchers to identify and understand complex relationships within the system.

Main effects plots, on the other hand, illustrate the individual impact of each factor on the response variable, providing a visual representation of the main effects.

These plots can aid in quickly identifying the most influential factors and assessing the relative importance of each factor in the experimental domain.

Advantages and Limitations of Full Factorial Design

While the full factorial design offers numerous advantages in terms of comprehensiveness and insight, it is important to recognize its limitations and potential drawbacks.

Understanding both the strengths and limitations of this experimental approach is crucial for making informed decisions and optimizing the trade-offs between resource allocation and the desired level of process understanding.

Advantages of Full Factorial Design

One of the primary advantages of the full factorial design is its ability to provide comprehensive insights into the system under investigation.

By considering all possible factor combinations, researchers can obtain a complete picture of the main effects, interactions, and potential curvature in the response surface, leading to a thorough understanding of the process dynamics.

Unlike some experimental designs that may overlook or confound interactions, the full factorial design explicitly accounts for interactions between factors.

This capability is particularly valuable in complex systems where the effect of one factor may depend on the level of another factor, allowing researchers to unravel these intricate relationships and optimize processes accordingly.

With a comprehensive understanding of the main effects and interactions, full factorial experiments enable researchers to estimate the optimal settings for the independent variables, leading to the best possible outcome for the response variable.

This optimization potential is invaluable in various industries, where process efficiency, product quality, and cost-effectiveness are paramount.

Limitations of Full Factorial Design

One of the primary limitations of the full factorial design is its resource-intensive nature.

As the number of factors and levels increases, the number of experimental runs required grows exponentially, leading to higher costs, longer experimental durations, and greater logistical challenges.

Related to the resource-intensive aspect, full factorial designs often require large sample sizes to ensure statistical validity and reliable estimates of main effects and interactions.

This can be particularly challenging in situations where resources are limited or experimental conditions are difficult to replicate.

The comprehensiveness of the full factorial design can also lead to an overwhelming amount of data, especially when dealing with numerous factors and levels.

Analyzing and interpreting such large datasets can be a daunting task, requiring advanced statistical techniques and computational resources.

Alternative Designs and Extensions

While the full factorial design is a powerful and comprehensive experimental strategy, some alternative designs and extensions can be employed depending on the specific requirements and constraints of the research or industrial application.

These alternative approaches can offer trade-offs between experimental complexity, resource requirements, and the level of information obtained.

Fractional Factorial Designs

Fractional factorial designs are a class of experimental designs that involve studying only a carefully chosen fraction of the full factorial design.

By sacrificing the ability to estimate certain higher-order interactions, fractional factorial designs can significantly reduce the number of experimental runs required, making them more resource-efficient.

Fractional factorial designs are particularly useful in screening experiments, where the primary goal is to identify the most influential factors before conducting more detailed investigations.

These designs can help researchers prioritize their efforts and allocate resources more effectively.

Response Surface Methodology

Response Surface Methodology (RSM) is a collection of statistical techniques used to model and optimize processes with multiple input variables.

The Central Composite Design (CCD) is a widely used RSM design that combines a factorial design with additional axial and center points, allowing for the estimation of quadratic effects and potential curvature in the response surface.

Another popular RSM design is the Box-Behnken Design, which is a spherical, rotatable, or nearly rotatable design.

This design is particularly efficient for exploring quadratic response surfaces and optimizing processes with three or more factors.

Unlike the Central Composite Design, the Box-Behnken Design does not include any points at the vertices of the cubic region defined by the upper and lower limits of the factors.

Taguchi Methods

Developed by Genichi Taguchi, the Taguchi methods are a set of techniques for robust parameter design and quality improvement.

One of the key elements of the Taguchi approach is the use of orthogonal arrays, which are a special class of fractional factorial designs.

Orthogonal arrays allow for the simultaneous investigation of multiple factors with a minimal number of experimental runs, making them an attractive option when resources are limited.

The Taguchi methods emphasize the concept of robust parameter design, which aims to identify factor-level combinations that minimize the variability in the response variable while achieving the desired target value.

This approach is particularly valuable in manufacturing and product development, where robustness to environmental and operational variations is critical for maintaining consistent performance and quality.

Conclusion

The full factorial design stands as a potent experimental strategy.

Considering every factor combination furnishes holistic comprehension of effects, interplays, and nonlinearities.

This lights pathways empowering better comprehension and optimization across varied sectors.

Advancing capabilities and statistical techniques envision expanding factorial applications.

Machine learning may analyze data efficiently while adaptive designs responsively calibrate based on real-time insights.

Additionally, sustainability priorities could drive factor prioritizations maximizing resource optimization and lessening environmental impacts.

Full factorials offer rigorous yet flexible methods unlocking enriched wisdom from intricate systems.

While exhaustive, generated learnings inspire noteworthy refinements throughout performance, quality, and workflows.

By following best practices, judiciously leveraging other designs, and tracking innovations, researchers and specialists harness factorials’ full gifts in driving innovations remarkably within respective realms.

Their gifts in illuminating intricate relations deserve recognition and prudent application wherever circumstances permit comprehensive experimentation.