Make Effective Decisions. Comprehensive Guide to Analytic Hierarchy Process (AHP)

Businesses regularly face tricky choices that could seriously impact how things run, profits, and long-term success.

Sorting through multiple angles, balancing different people’s goals, and uncertain results is hard work, especially when a lot hangs in the balance.

That’s where the Analytic Hierarchy Process (AHP) comes in handy, providing a methodical way to make decisions.

The AHP is a useful tool for analyzing complex problems. It assists decision-makers in lining up options and figuring out the best path using both hard numbers and softer factors.

Originally developed by Thomas Saaty back in the 1970s, Analytic Hierarchy Process (AHP) has since helped all sorts of fields like business, engineering, healthcare, and government tackle complicated puzzles. 

Breaking things down step-by-step offers a route towards well-informed solutions even when multiple moving pieces are involved.

Key Highlights

• Analytic Hierarchy Process (AHP) is a decision-making framework that considers multiple criteria and stakeholder perspectives.
• It employs a hierarchical structure to decompose complex problems into manageable components.
• Pairwise comparisons and Saaty’s scale allow for quantitative evaluation of subjective factors.
• Applications span various domains, including project portfolio selection, strategic planning, and resource allocation.
• Software tools, such as Expert Choice and Prioritization Helper, streamline the computational aspects of AHP.
• Best practices involve careful criteria selection, stakeholder involvement, and consistency checks.

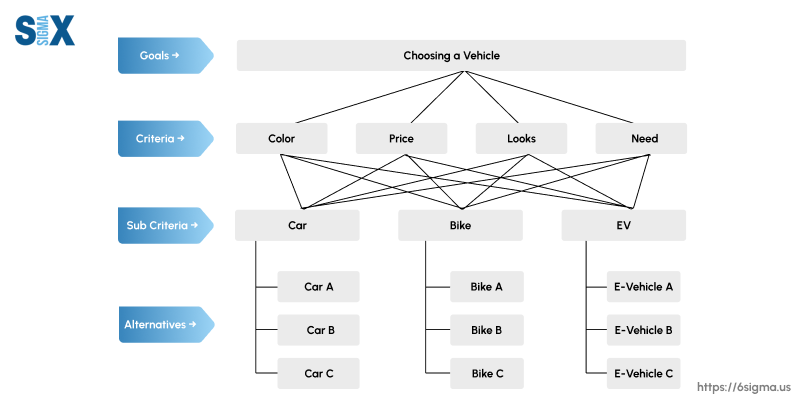
Analytic Hierarchy Process (AHP) breaks down complex problems into a hierarchical structure, consisting of the overall goal, criteria, sub-criteria, and alternatives. 

Providing a numerical ranking that reflects the preferences and priorities of the decision-maker AHP  leverages pairwise comparisons and mathematical principles, which quantifies the relative importance of each criterion and alternative.

Introduction to Analytic Hierarchy Process (AHP)

Companies often find themselves struggling with complex choices that can have far-reaching consequences. 

Navigating through a great number of criteria, conflicting stakeholder interests, and uncertain outcomes can be a daunting task, especially when the stakes are high. 

This is where the Analytic Hierarchy Process (AHP) comes in as a powerful ally, offering a structured and systematic approach to decision-making that transcends the limitations of traditional methods.

Multi-criteria Decision Analysis

AHP is a multi-criteria decision analysis (MCDA) technique that powers decision-makers to evaluate and prioritize alternatives based on both qualitative and quantitative factors. 

By breaking down complex problems into a hierarchical structure, Analytic Hierarchy Process (AHP) facilitates a comprehensive understanding of the various elements involved, including the overarching goal, criteria, sub-criteria, and potential alternatives.

Prioritization of Alternatives

One of the key strengths of Analytic Hierarchy Process is the ability to prioritize alternatives through a precise and objective process. 

By using pairwise comparisons and mathematical principles, AHP quantifies the relative importance of each criterion and alternative, ultimately providing a numerical ranking that reflects the decision-makers preferences and priorities. 

This ranking serves as a powerful tool for companies to make informed choices that align with their strategic objectives.

Decision-making Technique

Developed by Thomas L. Saaty in the 1970s at the Wharton School of the University of Pennsylvania, AHP has evolved into a widely recognized and respected decision-making technique. 

Its versatility and robustness have made it a go-to solution for organizations across various industries, including business, engineering, healthcare, and government sectors, where complex decisions are a constant challenge.

Group Decision-making

One of the key strengths of AHP is its ability to facilitate group decision-making. By consolidating diverse opinions and perspectives from multiple stakeholders, AHP provides a platform for collaborative decision-making processes. 

Through structured pairwise comparisons and mathematical calculations, AHP synthesizes the collective wisdom of the group, ensuring that the final decision reflects a well-rounded and inclusive approach.

Analytic Hierarchy Process (AHP) Fundamentals and Methodology

AHP has a detailed methodology that enables decision-makers to navigate through the complexities of multi-criteria decision-making. 

This methodology is grounded in a hierarchical structure, pairwise comparisons, and mathematical principles that translate subjective judgments into quantitative rankings.

Decision Hierarchies

The first step in the AHP process is to structure the decision problem into a hierarchical framework. 

This hierarchy typically consists of three levels: the overall goal or objective at the top, the criteria and sub-criteria that define the decision-making parameters in the middle, and the potential alternatives at the bottom. 

By cracking down the problem into manageable components, Analytic Hierarchy Process facilitates a clear understanding of the decision elements and their relationships.

Pairwise Comparison

Once the decision hierarchy is established, AHP employs a series of pairwise comparisons to evaluate the relative importance of each criterion and alternative. 

Decision-makers are asked to compare pairs of criteria or alternatives based on a predefined scale, often referred to as Saaty’s scale. 

This scale ranges from 1 (equal importance) to 9 (extreme importance), allowing for a quantitative assessment of subjective preferences.

Saaty’s Scale

Developed by Thomas Saaty, the founder of AHP, Saaty’s scale is a fundamental component of the pairwise comparison process. This scale provides a numerical representation of the relative importance or preference between two elements, such as criteria or alternatives. 

By assigning values from 1 to 9, decision-makers can express the intensity of their preferences, with 1 representing equal importance and 9 representing extreme importance.

Consistency Ratio

While AHP relies on subjective judgments, it also incorporates measures to ensure the consistency and validity of the decision-making process. 

The consistency ratio is a crucial metric that evaluates the coherence of the pairwise comparisons made by decision-makers. 

A low consistency ratio indicates a high level of consistency, increasing the reliability of the final decision. 

Conversely, a high consistency ratio may suggest inconsistencies in the judgments, prompting decision-makers to revisit their evaluations.

Eigenvector Calculation

AHP’s mathematical foundation lies in the eigenvector calculation. This calculation involves transforming the pairwise comparison matrices into numerical weights or priorities for each criterion and alternative. 

The resulting eigenvector represents the relative importance or preference of each element within the decision hierarchy, serving as the basis for the final ranking of alternatives.

Weighted-sum Model

The final step in the AHP process is the integration of the derived weights and priorities into a weighted-sum model.

This model combines the relative importance of each criterion with the performance scores of the alternatives, resulting in an overall score or ranking for each alternative. 

The alternative with the highest overall score is considered the optimal choice based on the decision-makers’ preferences and the defined criteria.

Analytic Hierarchy Process (AHP) Software and Tools

While the mathematical foundations of AHP are robust, the computational aspects can be complex, especially when dealing with large decision hierarchies and numerous pairwise comparisons. 

To streamline the process and ensure accuracy, various software tools and applications have been developed to support the implementation of AHP. 

Expert Choice Software

Expert Choice is a widely recognized and industry-leading software solution for AHP implementations. Developed by Expert Choice Inc., this software provides a user-friendly interface for constructing decision hierarchies, conducting pairwise comparisons, and analyzing the results.

Expert Choice automates the calculations and consistency checks, making it a valuable tool for organizations seeking to leverage the power of AHP in their decision-making processes. 

Prioritization Helper

Prioritization Helper is another popular AHP software solution, specifically designed for Salesforce users. 

This cloud-based application seamlessly integrates with the Salesforce platform, enabling decision-makers to conduct AHP analysis within their familiar Salesforce environment. 

Prioritization Helper’s intuitive interface and real-time calculations make it a powerful tool for streamlining decision-making processes within organizations that utilize Salesforce. 

PAPRIKA method

While Analytic Hierarchy Process is a widely adopted approach, alternative methods have been developed to address some of its limitations. 

The PAPRIKA (Potentially All Pairwise RanKings of all possible Alternatives) method is one such alternative, designed to be more cognitively simple and user-friendly. 

Instead of relying on ratio-scale measurements, PAPRIKA employs ordinal comparisons and choice-based questions, making the decision-making process more natural and accessible for decision-makers.

Criteria and Factors in Analytic Hierarchy Process

One of the key strengths of the Analytic Hierarchy Process lies in its ability to incorporate and evaluate a wide range of criteria and factors that influence decision-making. 

By breaking down complex problems into a hierarchical structure, AHP enables decision-makers to systematically consider and prioritize various elements that are critical to the decision at hand. 

These criteria and factors can span across multiple domains, including financial, strategic, risk-related, stakeholder-centric, and technical considerations.

Financial Criteria

In many decision-making scenarios, financial factors play a pivotal role. Analytic Hierarchy Process provides a framework to incorporate and prioritize financial criteria such as return on investment (ROI), net present value (NPV), payback period, and cost-benefit ratios. 

By quantifying these financial metrics, AHP allows organizations to evaluate the economic viability and profitability of potential alternatives, ensuring alignment with their financial objectives.

Strategic alignment

Aligning decisions with an organization’s strategic goals is crucial for long-term success. AHP enables decision-makers to include strategic criteria that reflect the organization’s vision, mission, and competitive positioning. 

These criteria may encompass factors such as market penetration, innovation, operational efficiency, and customer satisfaction, ensuring that the chosen alternative aligns with the organization’s overarching strategy.

Every decision carries inherent risks, and AHP provides a framework for assessing and prioritizing risk-related factors. 

Decision-makers can incorporate criteria such as operational risks, regulatory compliance risks, reputational risks, and environmental risks. 

Successful decision implementation often hinges on stakeholder buy-in and commitment. Analytic Hierarchy Process allows decision-makers to consider stakeholder-centric criteria, such as customer commitment, employee engagement, community support, and regulatory body approval. 

By prioritizing these factors, AHP ensures that the chosen alternative aligns with stakeholder interests and increases the likelihood of successful adoption and implementation.

Technical knowledge

In many industries, technical considerations play a crucial role in decision-making processes. AHP accommodates the inclusion of criteria related to technical knowledge, expertise, and capabilities. 

Decision-makers can evaluate factors such as the availability of skilled personnel, access to specialized equipment, technological advancements, and compatibility with existing systems, ensuring that the chosen alternative is feasible and sustainable from a technical standpoint.

Calculating Priorities and Inconsistencies with Analytic Hierarchy Process (AHP)

While the Analytic Hierarchy Process provides a structured framework for decision-making, its effectiveness relies heavily on the consistency and validity of the pairwise comparisons made by decision-makers. 

AHP incorporates several methods and techniques to calculate priorities and assess inconsistencies, ensuring the reliability and robustness of the final decision.

Consistency ratio

The consistency ratio is a critical measure in Analytic Hierarchy Process that evaluates the coherence and transitivity of the pairwise comparisons made by decision-makers. 

A low consistency ratio indicates a high degree of consistency, increasing confidence in the final decision. 

On the other hand, a high consistency ratio may suggest inconsistencies in the judgments, prompting decision-makers to revisit their evaluations and potentially refine their pairwise comparisons.

Inconsistency index

Closely related to the consistency ratio, the inconsistency index is another measure used in AHP to quantify the level of inconsistency in the pairwise comparison matrices. 

This index is based on the maximum eigenvalue of the comparison matrix and provides a numerical representation of the degree of inconsistency. 

Decision-makers can use this index to identify and address potential inconsistencies, enhancing the overall validity of the decision-making process.

Eigenvalue method

AHP’s mathematical foundation is the eigenvalue method, which is used to derive the priority vectors or weights from the pairwise comparison matrices. 

This method involves calculating the principal eigenvalue and eigenvector of the comparison matrix, representing the relative importance or preference of each criterion or alternative within the decision hierarchy.

Judgment quantification

One of the key strengths of AHP lies in its ability to quantify subjective judgments and preferences. 

Through the pairwise comparison process and the use of Saaty’s scale, AHP translates qualitative assessments into numerical values, allowing for a structured and quantitative evaluation of decision elements. 

This judgment quantification enables decision-makers to incorporate both tangible and intangible factors into the decision-making process.

Reciprocal comparisons

AHP relies on the principle of reciprocal comparisons, which ensures consistency and logical coherence in the pairwise comparison process. 

If a decision-maker judges that criterion A is X times more important than criterion B, then the reciprocal value (1/X) is automatically assigned to the comparison of criterion B concerning criterion A. 

This reciprocal relationship helps maintain consistency and reduces the potential for conflicting judgments.

Applications of Analytic Hierarchy Process

The Analytic Hierarchy Process has found widespread application across various domains and industries, owing to its versatility and ability to handle complex, multi-criteria decision problems. 

From project portfolio selection to resource allocation and strategic planning, AHP has proven to be a valuable tool for decision-makers seeking structured and data-driven approaches to decision-making.

Portfolio project selection

One of the most prominent applications of Analytic Hierarchy Process is in the realm of project portfolio management. Organizations often face the challenge of selecting and prioritizing projects from a pool of potential initiatives, each with its own set of benefits, costs, risks, and alignment with strategic objectives. 

AHP provides a systematic framework for evaluating and ranking these projects based on multiple criteria, ensuring that the selected portfolio aligns with the organization’s goals and maximizes resource utilization.

Ratio scale measurement

AHP’s reliance on pairwise comparisons and Saaty’s scale allow for the quantification of subjective judgments using ratio scales. 

This ratio scale measurement approach enables decision-makers to express the relative importance or preference between criteria and alternatives using a numerical scale, facilitating a more structured and quantitative evaluation process.

Decision matrix

AHP generates decision matrices that represent the pairwise comparisons and prioritization of criteria and alternatives. 

These decision matrices provide a detailed overview of the decision elements, their relative importance, and their contributions to the overall decision. 

Sensitivity analysis

One of the key advantages of Analytic Hierarchy Process is its ability to perform sensitivity analysis, which allow decision-makers to evaluate the impact of changing priorities or criteria weights on the final decision outcome. 

By varying the relative importance of different criteria or introducing new alternatives, decision-makers can assess the robustness and stability of their decisions, enabling them to make informed and resilient choices.

Comparison of Analytic Hierarchy Process (AHP) with Other Methods

While the Analytic Hierarchy Process has established itself as a prominent decision-making framework, it is not the only approach available to decision-makers. 

In recent years, alternative methods have emerged, each with its unique strengths and limitations. Practitioners need to understand and compare these methods to make informed choices about the most suitable approach for their specific decision-making needs.

PAPRIKA method

One alternative to AHP that has gained traction is the PAPRIKA (Potentially All Pairwise RanKings of all Possible Alternatives) method. 

Developed as a more cognitively simple and user-friendly approach, PAPRIKA relies on ordinal comparisons and choice-based questions rather than ratio-scale measurements. 

Instead of asking decision-makers to quantify the relative importance of criteria and alternatives using a numerical scale, PAPRIKA presents hypothetical scenarios involving trade-offs between pairs of alternatives defined by two criteria at a time.

This approach is designed to be more intuitive and aligned with the natural decision-making processes that individuals encounter in their daily lives. 

While PAPRIKA aims to address some of the cognitive challenges associated with AHP, it still relies on pairwise comparisons and may not be suitable for all decision-making contexts.

Ratio scale measurement

One of the distinguishing features of AHP is its reliance on ratio scale measurements, which allow decision-makers to express the relative importance or preference between criteria and alternatives using a numerical scale (Saaty’s scale). 

This approach enables a quantitative evaluation of subjective judgments and facilitates the mathematical calculations involved in deriving priorities and rankings.

Best Practices and Guidelines

To maximize the effectiveness and reliability of the Analytic Hierarchy Process, it is crucial to follow best practices and guidelines throughout the decision-making process. 

These practices help ensure that the decision is well-informed, inclusive, and based on consistent and valid judgments, ultimately increasing the likelihood of successful implementation and desired outcomes.

Criteria selection

The selection of appropriate criteria and sub-criteria is a critical first step in the AHP process. 

Decision-makers must carefully identify and define the relevant criteria that accurately reflect the organization’s objectives, stakeholder interests, and decision-making context. 

Stakeholder involvement

Effective decision-making often requires the involvement and buy-in of multiple stakeholders, each with their unique perspectives and priorities. 

AHP provides a structured framework for incorporating diverse stakeholder opinions through group decision-making processes. 

Consistency checks

As discussed earlier, consistency is a crucial aspect of the AHP process. Decision-makers should regularly perform consistency checks to ensure the logical coherence and transitivity of their pairwise comparisons. 

By monitoring consistency ratios and inconsistency indices, decision-makers can identify and address potential inconsistencies, enhancing the validity and reliability of their judgments.

Conclusion

The Analytic Hierarchy Process proves a powerful and flexible tool for tackling complicated choices from multiple angles. By blending math concepts with organized decision-making steps, Analytic Hierarchy Process helps teams determine options while weighing tangible and softer factors against their strategic aims.

It succeeds by breaking problems down into clear levels, getting different views by comparing items side by side and quantifying more subjective views into clear priorities. 

This gives a logical, evidence-based approach to choices while earning support from those involved.

While AHP has strengths, it’s important to acknowledge limits too, like other methods working better sometimes. By learning different strategies, decision-makers choose what fits their specific situations best.

Ultimately, using any such framework relies on doing it right – like carefully selecting what matters, including stakeholders, and double-checking consistency. 

By following guidelines and tapping into AHP’s strengths, teams can handle complex calls with confidence, all pointing toward goals and success.

Even so, Analytic Hierarchy Process remains a handy tool in any decision-maker’s toolkit for enabling thoughtful, careful choices leading to growth, innovation, and sustainability in the long run. With care and skill, it empowers smart decisions with impacts.