Articles

Six Sigma revolutionized manufacturing and service industries by introducing statistical methods to reduce defects and optimize processes.

This methodology relies heavily on data analysis and hypothesis testing to validate improvements and make informed decisions.

Why Hypothesis Testing Matters in Six Sigma

In the Six Sigma framework, hypothesis testing serves as a critical tool for process improvement teams.

When organizations implement changes or improvements, they need concrete evidence to support their decisions.

Alternative hypothesis in Six Sigma provides this evidence by helping teams determine if observed changes are statistically significant or merely due to random variation.

What You’ll Learn

• Alternative Hypothesis Formulation and Testing
• Statistical Tools for Hypothesis Analysis
• Real Process Improvement Applications
• Data-Driven Decision Making Methods

Six Sigma and Hypothesis Testing

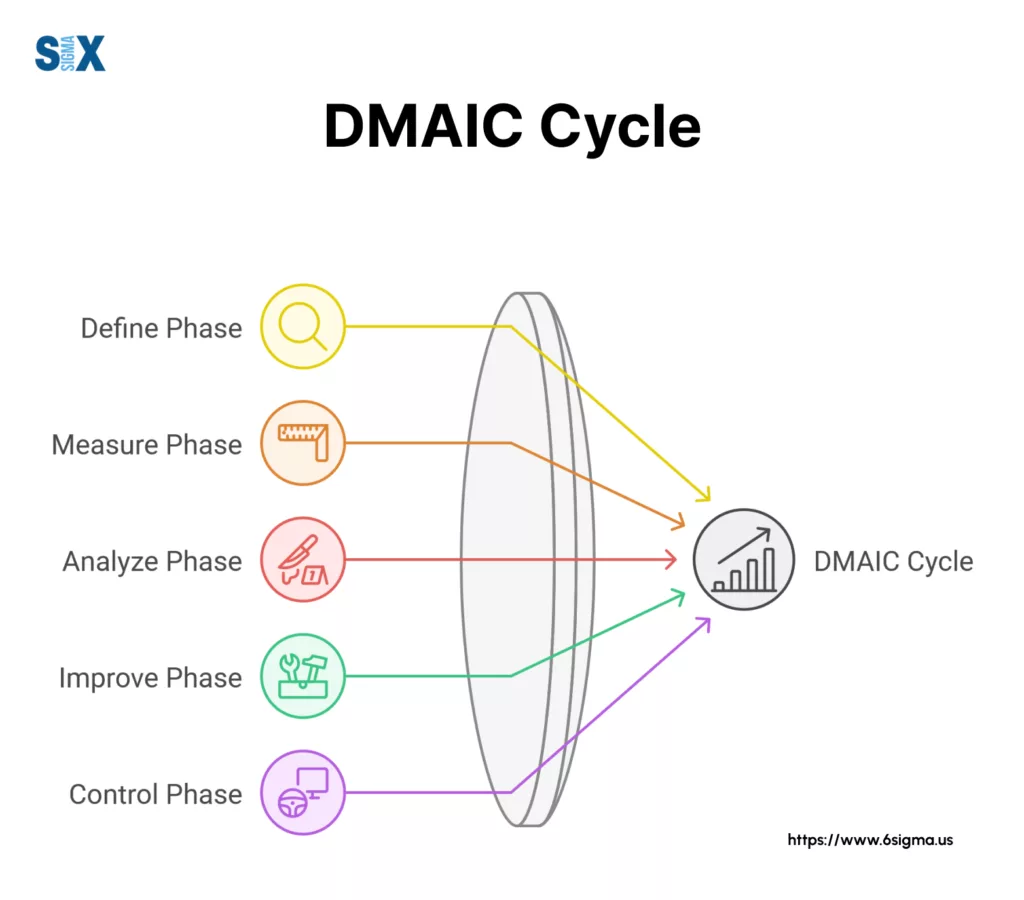
Six Sigma methodology focuses on reducing process variation and eliminating defects through statistical analysis.

This data-driven approach uses the DMAIC framework – Define, Measure, Analyze, Improve, and Control – to solve complex business problems and enhance process performance.

Statistical Analysis: The Backbone of Six Sigma

Statistical analysis drives decision-making in Six Sigma projects. Teams use alternative hypothesis in statistics to validate process changes and improvements.

When analyzing data, practitioners must distinguish between random variation and significant process changes. This is where alternative hypothesis testing becomes crucial.

For example, a manufacturing team might test whether a new machine setting reduces defect rates.

The alternative hypothesis statistics would help determine if the observed improvement is statistically significant or just coincidental.

Hypothesis Testing in Process Improvement

Hypothesis testing serves as a critical tool throughout the DMAIC phases. During the Analyze phase, teams use alternative hypothesis in Six Sigma to:

• Verify root causes of problems
• Test relationships between variables
• Validate improvement ideas
• Confirm process changes

The statistical rigor of hypothesis testing ensures that process improvements are based on facts rather than assumptions.

Quality improvement professionals rely on these tests to make informed decisions about process changes, resource allocation, and improvement strategies.

Modern Applications in Industry

Today’s Six Sigma projects integrate hypothesis testing with digital tools and software platforms. Teams can now perform complex statistical analyses faster and more accurately.

This evolution has made alternative hypothesis testing more accessible while maintaining its statistical power and reliability.

What Is An Alternative Hypothesis?

The alternative hypothesis represents a statement that suggests a significant difference or change exists in a process or population.

In Six Sigma projects, this hypothesis typically proposes that a process improvement or change has created a measurable effect.

The alternative hypothesis definition stands in direct opposition to the null hypothesis, which assumes no significant change has occurred.

The Null-Alternative Relationship

Think of the null and alternative hypothesis as two sides of the same coin. While the null hypothesis states that no change or relationship exists, the alternative hypothesis suggests otherwise.

For example, if a Six Sigma team implements a new manufacturing process, the alternative hypothesis might state that the new process reduces defects, while the null hypothesis would claim no improvement in defect rates.

Statistical Significance and Decision Making

The alternative hypothesis plays a crucial role in statistical analysis by providing a framework for testing process improvements.

When teams collect and analyze data, they use statistical tests to determine whether they should reject the null hypothesis in favor of the alternative hypothesis.

This decision-making process helps ensure that observed improvements are genuine rather than random variations.

Notation and Technical Expression

In statistical documentation, the alternative hypothesis is typically denoted as H1 or Ha. This notation helps distinguish it from the null hypothesis (H0) in formal analysis and reporting.

The technical expression of an alternative hypothesis can take several forms:

• Directional (one-tailed): μ > μ0 or μ < μ0
• Non-directional (two-tailed): μ ≠ μ0

Where μ represents the process mean after improvement, and μ0 represents the original process mean.

Types of Alternative Hypotheses

One-Tailed Hypothesis Testing

One-tailed tests examine changes in a specific direction. An alternative hypothesis example in this category might state that a new manufacturing process reduces defect rates below the current level.

This type proves particularly useful when Six Sigma teams need to verify specific improvements or degradations in process performance.

Two-Tailed Hypothesis Testing

Two-tailed tests investigate changes in either direction. For instance, when implementing a process change, teams might test whether the modification affects cycle time, regardless of whether it increases or decreases.

This approach offers more flexibility but requires larger sample sizes for statistical significance.

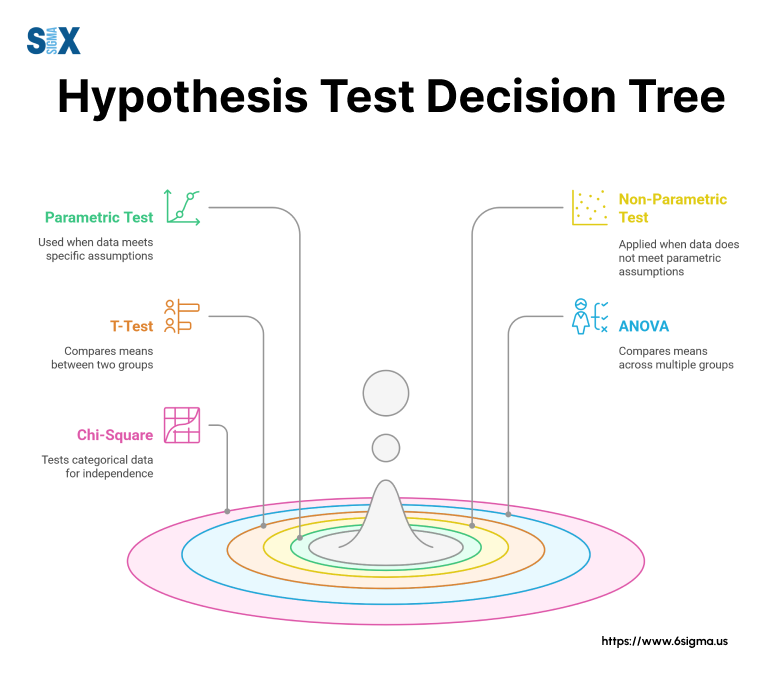
Directional vs. Non-Directional Testing

Directional hypotheses specify the expected direction of change. Consider a Six Sigma project aimed at reducing customer wait times. The alternative hypothesis examples might include:

Directional: “The new service process reduces average wait time below 10 minutes”
Non-directional: “The new service process changes average wait time from 10 minutes”

Selecting the Right Type

The choice between hypothesis types depends on project goals and available data.

When teams have strong evidence suggesting improvement in a specific direction, one-tailed tests offer greater statistical power.

However, two-tailed tests provide safer options when the direction of change remains uncertain.

Formulating Alternative Hypotheses in Six Sigma

Writing an alternative hypothesis in Six Sigma requires careful consideration of process metrics and improvement goals.

Start by identifying the specific process parameter you want to improve. Next, define the current performance level and the expected change.

Finally, express this change in statistical terms using the alternative hypothesis formula.

Creating Clear Hypothesis Statements

How to write an alternative hypothesis effectively begins with precise language.

For manufacturing processes, state the expected improvement specifically: “The modified assembly process reduces defect rates from 3% to 1%.” This clarity helps teams measure and validate improvements accurately.

Six Sigma Project Considerations

Six Sigma projects demand rigorous statistical analysis.

When formulating hypotheses, consider:

• Process capability requirements
• Customer specifications
• Measurement system accuracy
• Sample size availability
• Project timeline constraints

Avoiding Common Pitfalls

Many teams make mistakes when developing alternative hypotheses.

Watch out for:

• Vague statements: “The process will improve” lacks specificity
• Unmeasurable claims: Ensure all parameters can be quantified
• Unrealistic expectations: Stay within practical improvement limits
• Multiple variables: Focus on one improvement aspect at a time

Validation and Review

Before proceeding with testing, verify that your alternative hypothesis aligns with:

• Project goals and objectives
• Available measurement capabilities
• Statistical testing requirements
• Stakeholder expectations

Alternative Hypothesis in Six Sigma Applications

A major automotive parts manufacturer applied alternative hypothesis testing to optimize their production line.

The team formulated an alternative null hypothesis stating that new tooling settings would reduce dimensional variations.

After collecting data over three months, statistical analysis led them to accept the alternative hypothesis, confirming a 40% reduction in part variations.

Quality Control Implementation

In pharmaceutical packaging, quality teams use hypothesis testing to validate inspection systems. One notable project examined defect detection rates.

The alternative hypothesis proposed that automated inspection would identify 99.9% of defects, compared to 98.5% with manual inspection.

The data supported this claim, revolutionizing their quality control process.

Customer Satisfaction Metrics

Service industries leverage alternative hypothesis in Six Sigma projects to enhance customer experience. A telecommunications company tested whether their new customer service protocol improved satisfaction scores.

The hypothesis testing revealed a statistically significant improvement, leading to widespread implementation across all service centers.

Defect Reduction Success Stories

A semiconductor manufacturer tackled yield issues through systematic hypothesis testing.

Their alternative hypothesis stated that modified cleaning procedures would reduce contamination levels.

The results showed a remarkable 60% decrease in defect rates, prompting similar improvements across multiple production lines.

Data-Driven Decision Making

These applications demonstrate how teams use hypothesis testing to drive improvements. When projects properly structure and test hypotheses, they:

• Validate process changes
• Quantify improvements
• Support investment decisions
• Guide implementation strategies

Common Challenges and Solutions

Result Interpretation Pitfalls

Teams often struggle with determining whether to reject or accept the alternative hypothesis. Statistical significance doesn’t always equal practical importance.

For example, a process change might show statistical significance but offer minimal real-world impact. The correct alternative hypothesis must balance statistical validity with practical benefits.

Significance Level Selection

Choosing appropriate significance levels impacts decision quality. While 0.05 serves as a standard threshold, Six Sigma projects might require stricter levels for critical processes.

Manufacturing safety components, for instance, might demand 0.01 significance levels to minimize risk.

Managing Conflicting Data

When data sets produce contradictory results, teams must investigate underlying causes. This might involve:

• Measurement system analysis
• Sample size verification
• Process stability checks
• Environmental factor assessment

These challenges highlight why teams must maintain statistical rigor while considering practical implications in Six Sigma projects.

Regular validation and careful analysis ensure reliable conclusions from hypothesis testing efforts.

Moving Forward With Alternative Hypothesis Testing

Alternative hypothesis in Six Sigma serves as a fundamental tool for validating process improvements and driving data-based decisions.

From manufacturing floors to service operations, this statistical approach transforms theoretical concepts into measurable results.

The evolution of Six Sigma methodology continues to emphasize the critical role of hypothesis testing in process improvement.

Modern digital tools and software make these statistical methods more accessible, while maintaining the rigorous standards that define Six Sigma excellence.

Success in Six Sigma projects depends on proper hypothesis formulation, testing, and interpretation. Teams that master these concepts deliver more reliable improvements and sustainable results across industries.

The future of Six Sigma will see even greater integration of hypothesis testing with emerging technologies, making statistical analysis more powerful and user-friendly for practitioners at all levels.