< >

Statistical Design of Experiments Statistical Design of Experiments Unit VII Unit VII Robust Design Robust Design using using Taguchi Methods Taguchi Methods

Statistical Design of Experiments Statistical Design of Experiments Robust Design Robust Design

Statistical Design of Experiments Statistical Design of Experiments Robust Design Robust Design • • An engineering strategy for product/ An engineering strategy for product/ process designs process designs • • Can be applied from the start of R&D Can be applied from the start of R&D and Advanced Product/Process and Advanced Product/Process Design Design • • An efficient approach to generate An efficient approach to generate technical information technical information

Statistical Design of Experiments Statistical Design of Experiments Robust Design Robust Design • • Concentrates on Concentrates on » » Identifying ideal function(s) for Identifying ideal function(s) for product/process design product/process design » » Choosing the best levels for Choosing the best levels for product/process design parameters product/process design parameters that optimize performance, while that optimize performance, while minimizing sensitivity to variation minimizing sensitivity to variation (robustness), at lowest cost (robustness), at lowest cost

Statistical Design of Experiments Statistical Design of Experiments Design Phases Design Phases SYSTEM DESIGN PARAMETER DESIGN TOLERANCE DESIGN TIME DESIGN STABILITY Low High Primary Primary Focus of Focus of Robust Design Robust Design

Statistical Design of Experiments Statistical Design of Experiments Design Phases Design Phases • • System Design System Design ­ ­ Generating and Selecting concepts. Generating and Selecting concepts. ­ ­ Concept comparisons Concept comparisons ­ ­ Functional design focused on the Functional design focused on the pertinent Technology pertinent Technology ­ ­ No DOE occurs at this stage No DOE occurs at this stage • • System Design System Design • • Parameter Design Parameter Design – – A means of Both reducing costs and A means of Both reducing costs and improving quality by making effective use of improving quality by making effective use of experimental design methods experimental design methods – – Selecting values for design parameters Selecting values for design parameters which cause the system performance to be which cause the system performance to be insensitive to variations (or noise factors) insensitive to variations (or noise factors) – – This is the heart of Robust Design This is the heart of Robust Design • • System Design System Design • • Parameter Design Parameter Design • • Tolerance Design Tolerance Design – – Economic evaluation of tolerances Economic evaluation of tolerances – – Identifying those to tighten and those to relax Identifying those to tighten and those to relax – – After the system has been designed and the After the system has been designed and the nominal mid-values of its parameters nominal mid-values of its parameters determined, the next step is to determine the determined, the next step is to determine the tolerances of the parameters tolerances of the parameters

Statistical Design of Experiments Statistical Design of Experiments Why Robust Design? Why Robust Design? • Warranty Costs - Costs exceed target goals - Products sometimes fail to perform - Variation in product function is also a major contributor (lack of robustness) - any variation from the performance target is bad for the customer • • Warranty Costs... Warranty Costs... • • Product Cycle Time... Product Cycle Time... – – Need to reduce “design/development time” Need to reduce “design/development time” – – Need to improve new product reliability... Need to improve new product reliability... it’s never where it should be at ‘launch.’ it’s never where it should be at ‘launch.’ – – Design ‘refining’ is avoided when the        Design ‘refining’ is avoided when the        robustness robustness (sensitivity to variation) is (sensitivity to variation) is evaluated and known early evaluated and known early

Statistical Design of Experiments Statistical Design of Experiments Robust Design is... Robust Design is... • • 90% Engineering Strategy 90% Engineering Strategy • • 10% D.O.E.  (Testing) 10% D.O.E.  (Testing)

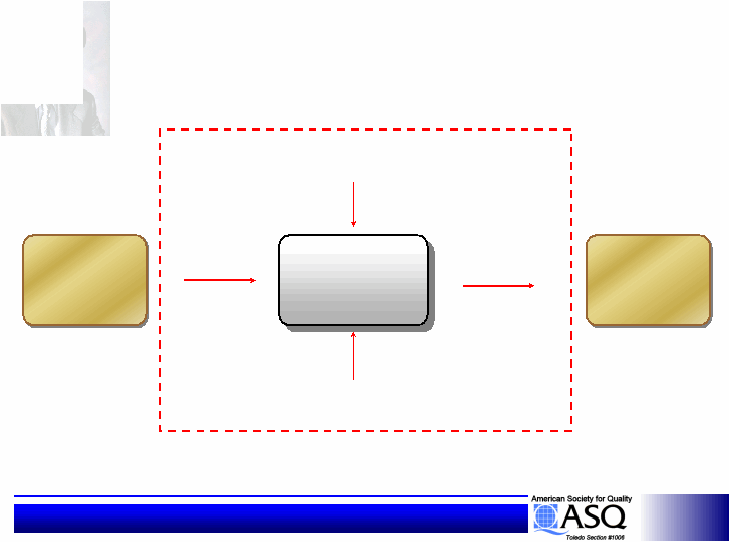Statistical Design of Experiments Statistical Design of Experiments Customer View - Customer View - Engineering View Engineering View Control factors Control factors System (Subsystem) System System (Subsystem) (Subsystem) Engineered System Input Input Signal Signal Customer Intent Customer Intent Perceived Result Perceived Result Noise Factors Noise Factors Output Output Response Response

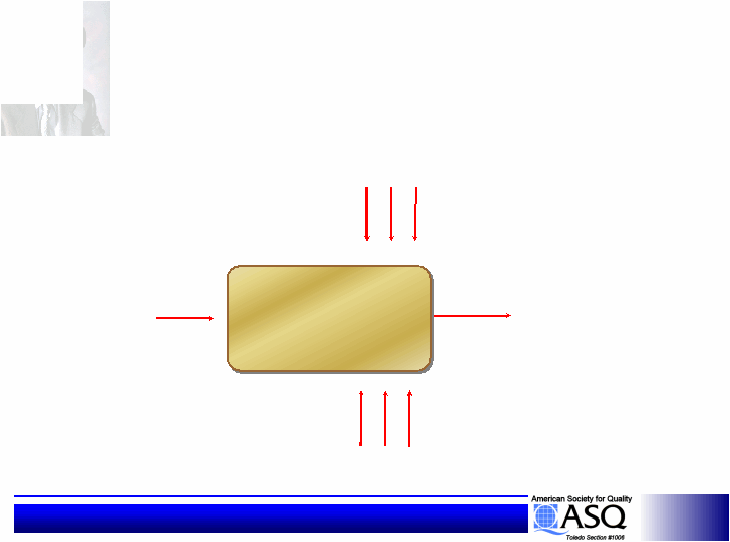Statistical Design of Experiments Statistical Design of Experiments Parameter Diagram Parameter Diagram SYSTEM SYSTEM INPUT INPUT SIGNAL SIGNAL OUTPUT OUTPUT RESPONSE RESPONSE CONTROL CONTROL FACTORS FACTORS NOISE NOISE FACTORS FACTORS A Framework for Describing the Engineered System

Statistical Design of Experiments Statistical Design of Experiments Control Factors Control Factors • • Design parameters of a system that: Design parameters of a system that: • • affect system performance, and affect system performance, and • • are specified by nominal values are specified by nominal values • • Examples include: Examples include: • • material  (chemical makeup, hardness) material  (chemical makeup, hardness) • • mechanical (pressures, flow rates) mechanical (pressures, flow rates) • • dimensional (length, width, roundness, dimensional (length, width, roundness, coating thickness) coating thickness) • • surface finish (smoothness) surface finish (smoothness)

Statistical Design of Experiments Statistical Design of Experiments Noise Factors Noise Factors • • Variables or parameters which: Variables or parameters which: • • affect system performance, and affect system performance, and • • are either uncontrollable or not are either uncontrollable or not economical to control economical to control • • Examples include: Examples include: • • material variation  (chemical makeup, material variation  (chemical makeup, strength) strength) • • environment (temperature, humidity) environment (temperature, humidity) • • Customer Application Customer Application

Statistical Design of Experiments Statistical Design of Experiments 3 Types of Noise 3 Types of Noise • • Customer usage Customer usage (External) (External) • • Maintenance practices Maintenance practices • • Geographic features Geographic features • • Duty cycle Duty cycleTolerances •Manufacturing •Manufacturing •Component Wear •Component Wear Processes Processes •Corrosion / Chemical •Corrosion / Chemical Equipment Equipment • • Material / Part Material / Part Tolerances •Aging (Internal) •Aging (Internal) • • • • Degradation Degradation • • Calibration Drift Calibration Drift

Statistical Design of Experiments Statistical Design of Experiments Noise factors are Important! Noise factors are Important! Loss to Society Loss to Society Loss to Society Deviations of System Performance from Target Value Deviations of Deviations of System Performance System Performance from Target Value from Target Value Noise Factors Cause Variations Noise Factors Noise Factors Cause Variations Cause Variations Product/Process Design Product/Process Design Product/Process Design

Statistical Design of Experiments Statistical Design of Experiments Noise Factors Cause Variations Noise Factors Noise Factors Cause Variations Cause Variations Outer Outer Noise Noise Variations in Variations in Operating Operating environment environment Human Error Human Error Manufacturer Manufacturer has least has least control control Inner Inner Noise Noise Between Between Product Product Noise Noise Deterioration Deterioration Material Material Wearout Wearout Manufacturing Manufacturing Imperfections Imperfections Unit to Unit Unit to Unit Process Process Gage R & R Gage R & R

Statistical Design of Experiments Statistical Design of Experiments Countermeasures for Noise Countermeasures for Noise • • Ignore Them... Ignore Them... - - Could result in fire fighting later on. Could result in fire fighting later on. • • Control or Eliminate Them... Control or Eliminate Them... - - Standardization Standardization - - Failsafing Failsafing - - Eliminating the cause may be expensive. Eliminating the cause may be expensive. -- - Noise factor becomes a control factor. Noise factor becomes a control factor. • • Compensate for Effects of Compensate for Effects of Noise... Noise... - - Feedback controls in manufacturing Feedback controls in manufacturing or the product. or the product. - - Adds complexity. Adds complexity. - - Noise factor becomes a signal.The focus of Robust Design Noise factor becomes a signal.The focus of Robust Design • • Minimize the Effects of Noise... Minimize the Effects of Noise... - - Most cost effective approach Most cost effective approach - - Select design parameter values so Select design parameter values so the system is least sensitive to the system is least sensitive to noises noises -

Statistical Design of Experiments Statistical Design of Experiments Auto Brake System Example Auto Brake System Example Energy Transformations Energy Transformations Signal Slow vehicle down smoothly Slow vehicle down smoothly “Smooth” braking “Smooth” braking Response Noise Factors • Age of brakes • Road conditions • Ambient Temp. Control Factors • Brake Pad Mat’l • Rotor Material • Brake Fluid Torque • Pedal force

Statistical Design of Experiments Statistical Design of Experiments Ideal Thinking Ideal Thinking Energy Thinking Energy Thinking The ideal relationship The ideal relationship relationship between input between input signal and output response based on signal and output response based on the energy the energy or information transformation or information transformation of the system. of the system.

Statistical Design of Experiments Statistical Design of Experiments Ideal Function Ideal Function X: Input Signal Y: Output Response Y = f(X) Reality System • Brake pad • Motor • Coating Input Signal • Force • Wattage • Time    Output Response • Torque • Torque*Rpm • Thickness   Y X

Statistical Design of Experiments Statistical Design of Experiments Don’t focus on “Symptoms” Don’t focus on “Symptoms” • • Customers complain about “symptoms” Customers complain about “symptoms” • • often not the desired output of the system often not the desired output of the system • • Focus on the ideal, desired response: Focus on the ideal, desired response: • • maximize the desired response maximize the desired response • • avoid moving energy from one symptom to avoid moving energy from one symptom to another another

Statistical Design of Experiments Statistical Design of Experiments Auto Brake System with Auto Brake System with “Symptoms” “Symptoms” Energy Transformations Energy Transformations Signal Signal Slow vehicle down smoothly Slow vehicle down smoothly “Smooth” braking “Smooth” braking Response Response Undesired: Undesired: • • Squeal Squeal • • Wear Wear • • Vibrations Vibrations • • “Symptoms” “Symptoms” Noise Factors Noise Factors • • Age of brakes Age of brakes • • Road conditions Road conditions • • Ambient Temp. Ambient Temp. Control Factors Control Factors • • Brake Pad Mat’l Brake Pad Mat’l Mat’l • • Rotor Material Rotor Material • • Brake Fluid Brake Fluid Desired: Desired: Torque Torque • • Pedal Pedal force force

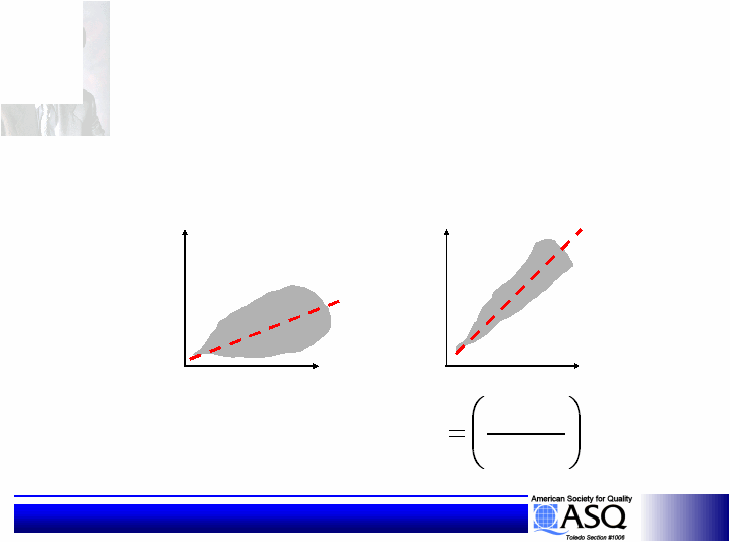Statistical Design of Experiments Statistical Design of Experiments Robustness Metric Robustness Metric S/N Ratio S/N Ratio Goal:  High S/N Goal:  High S/N Y Y Y Y X X X X Signal/Noise Ratio Signal/Noise Ratio noise signal F

Statistical Design of Experiments Statistical Design of Experiments Two Step Optimization Two Step Optimization An optimized product or process An optimized product or process requires performance with: requires performance with: • • small variation about the mean, and small variation about the mean, and • • the mean adjusted to the design the mean adjusted to the design target. target.

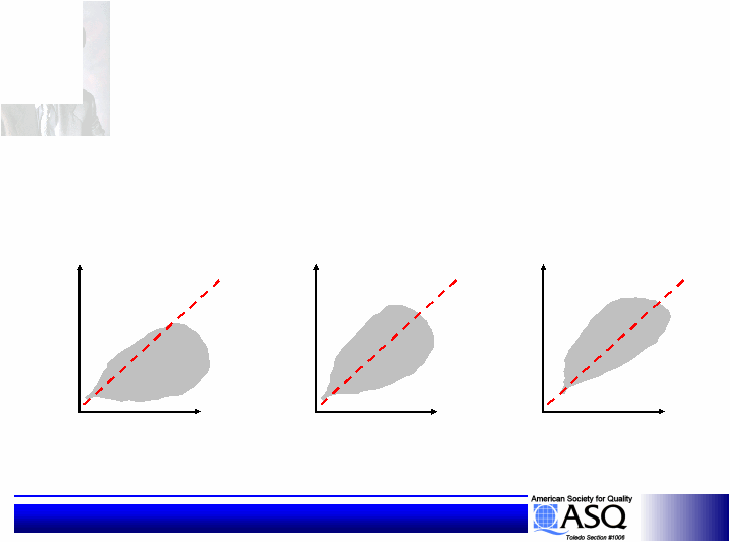Statistical Design of Experiments Statistical Design of Experiments Traditional Approach Traditional Approach 1) Design to the target. 1) Design to the target. 2) Reduce the variability. 2) Reduce the variability. initial design concept initial design concept optimized designs optimized designs Y Y X X target target Y Y X X target target Y Y X X target target

Statistical Design of Experiments Statistical Design of Experiments 1) Reduce the variability. 1) Reduce the variability. 2) Design to the target. 2) Design to the target. Y Y X X target target initial design concept initial design concept optimized designs optimized designs Y Y X X target target Y Y X X target target Robust Approach Robust Approach

Statistical Design of Experiments Statistical Design of Experiments Signal-to-Noise Definitions Signal-to-Noise Definitions Signal-to-Noise Analysis measures Signal-to-Noise Analysis measures variation within treatment variation within treatment combinations when noise is present. combinations when noise is present. Signal-to-Noise Analysis transforms all Signal-to-Noise Analysis transforms all treatment combination repetition data treatment combination repetition data to one value which is the measure of to one value which is the measure of variation present. variation present. Noise causes response variable results Noise causes response variable results to not be repeatable within a treatment to not be repeatable within a treatment combination. combination. Look at the repeatability within a Look at the repeatability within a treatment combination to treatment combination to determine the Signal-to-Noise determine the Signal-to-Noise Ratio. Ratio. S/N = S/N = Power of the Signal Power of the Signal Power of the noise Power of the noise Desire the power of the Desire the power of the signal to be great over signal to be great over the power of the noise the power of the noise The higher the S/N Ratio, the more the The higher the S/N Ratio, the more the system is robust (insensitive) to noise. system is robust (insensitive) to noise. Taguchi uses Design of Experiments to Taguchi uses Design of Experiments to determine where noise is affecting determine where noise is affecting response variable repeatability within a response variable repeatability within a treatment combination so that input treatment combination so that input factors can be optimized to decrease the factors can be optimized to decrease the uncontrollable noise effects. uncontrollable noise effects.

Statistical Design of Experiments Statistical Design of Experiments From Theory to Application From Theory to Application You’ve just learned You’ve just learned the basic background the basic background of Robust Design.  of Robust Design.  Now you’re ready to Now you’re ready to learn how to apply learn how to apply Robust Design Robust Design techniques in Day to techniques in Day to Day opportunities! Day opportunities!

Statistical Design of Experiments Statistical Design of Experiments Loss Function Loss Function Smaller - Smaller - the - the - Better Better L L O O S S S S I I N N $ T=O T=O L L / / Loss For Loss For One Piece One Piece L = K X² L = K X² 2 Oil Consumption, Wear, Smoke, etc Oil Consumption, Wear, Smoke, etc Recall Taguchi Loss Recall Taguchi Loss Function Function Philosophy Philosophy – – Reduce variation Reduce variation around target around target – – Determine Determine nominal target nominal target Smaller-the-Better Signal-to-Noise Smaller-the-Better Signal-to-Noise = -10 Log ( X I 2 / N) i=1 N

Statistical Design of Experiments Statistical Design of Experiments Loss Function Loss Function Larger - Larger - the - the - Better Better Life Span Life Span Interest Rate Interest Rate Fuel Economy Fuel Economy Crop Yield Crop Yield L L O O S S S S I I N N $ L L Loss For Loss For One Piece One Piece L = K (1/X L = K (1/X²) 2 ) n Larger-the-Better Signal-to-Noise Larger-the-Better Signal-to-Noise = -10 Log ( = -10 Log ( 1/X 1/X I I 2 2 / N) / N) i=1 i=1 N N

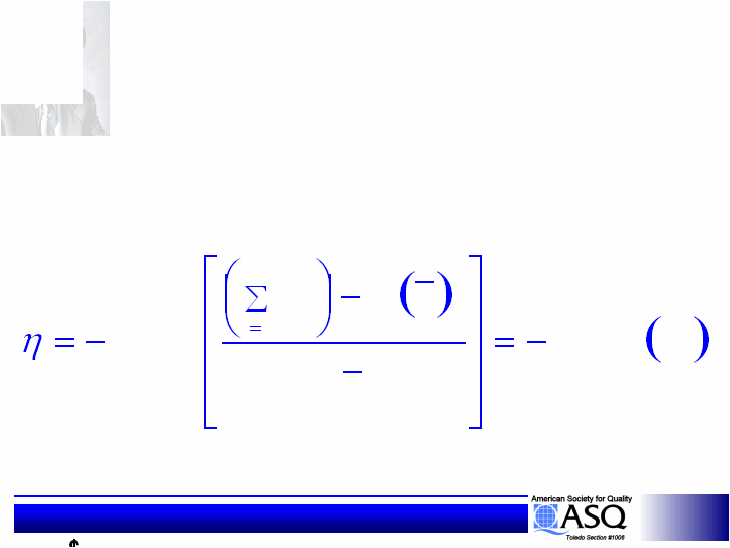Statistical Design of Experiments Statistical Design of Experiments Torque Torque Temp Temp Dimensional Dimensional Values Values Loss Function Loss Function Nominal - Nominal - is - is - Best Best L L O O S S S S I I N N L L T T X X Loss For Loss For One Piece             One Piece             L = K (X-T) L = K (X-T) -T) T)² 2 e e V N V y N 2 log 10 Nominal-the-Best Signal-to-Noise I Nominal-the-Best Signal-to-Noise I Nominal-the-Best Signal-to-Noise II Nominal-the-Best Signal-to-Noise II e N i i V N y N y log 10 1 log 10 2 1 2

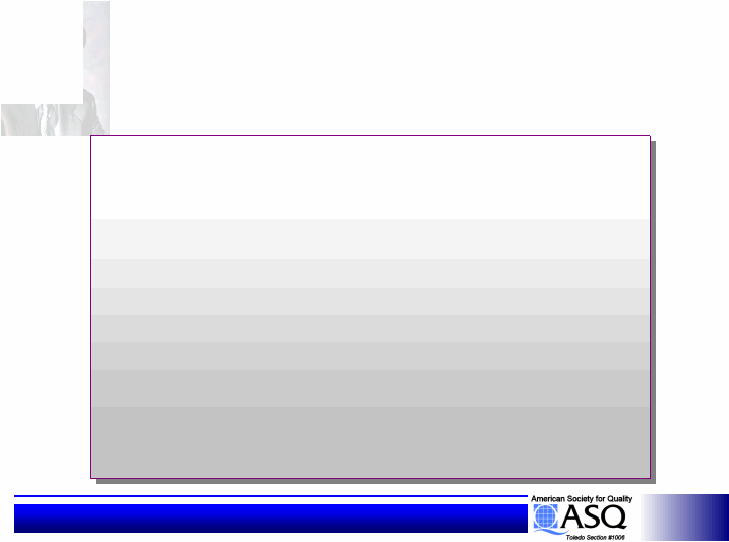Statistical Design of Experiments Statistical Design of Experiments 1. Define project scope/objectives 1 . Define project scope/objectives 2. Identify Ideal Function 2. Identify Ideal Function . Identify Ideal Function 3. Develop Signal & Noise Factor 3. Develop Signal & Noise Factor . Develop Signal & Noise Factor strategies strategies 4. Establish Control Factors and Levels 4. Establish Control Factors and Levels 5. Conduct Experiments or Simulations 5. Conduct Experiments or Simulations 6. Conduct Data Analysis 6 . Conduct Data Analysis 7. Conduct Confirmation Run 7. Conduct Confirmation Run . Conduct Confirmation Run 8. Implement & Document Results 8. Implement & Document Results . Implement & Document Results 8 Steps of Parameter Design 8 Steps of Parameter Design

Statistical Design of Experiments Statistical Design of Experiments Inner Arrays & Outer Arrays Inner Arrays & Outer Arrays Factors are generally divided into at least Factors are generally divided into at least two basic types: two basic types: Control factors are the factors which are Control factors are the factors which are to be optimized to attain the experimental to be optimized to attain the experimental goal.The optimum choice of control factor goal.The optimum choice of control factor Noise factors represent the Noise factors represent the uncontrollable elements of the system.  uncontrollable elements of the system.  levels should be robust over the noise levels should be robust over the noise factor levels. factor levels. 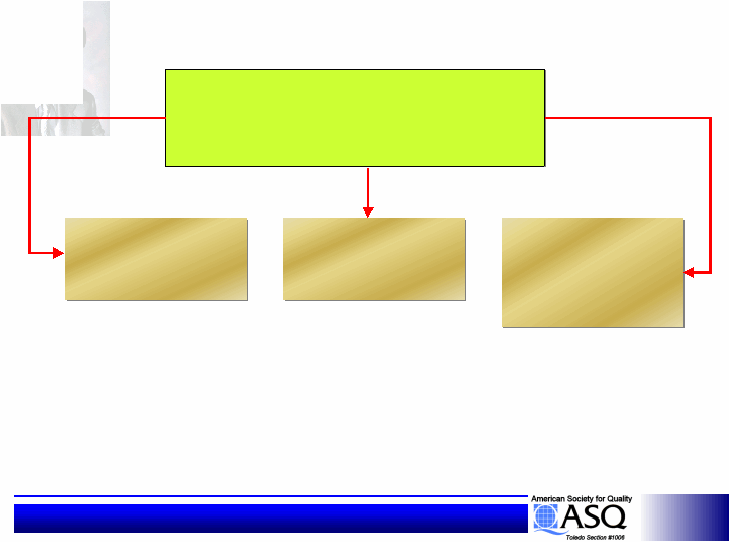Control and noise factors are usually handled Control and noise factors are usually handled differently in setting up an experiment.  differently in setting up an experiment.  Control factors are entered into an Control factors are entered into an orthogonal array called an inner array.  The orthogonal array called an inner array.  The noise factors are entered into a separate noise factors are entered into a separate array called an outer array.  These arrays are array called an outer array.  These arrays are so related that every testing set-up in the so related that every testing set-up in the -up in the up in the inner array is evaluated across every noise inner array is evaluated across every noise set-up in the outer array. set-up in the outer array.

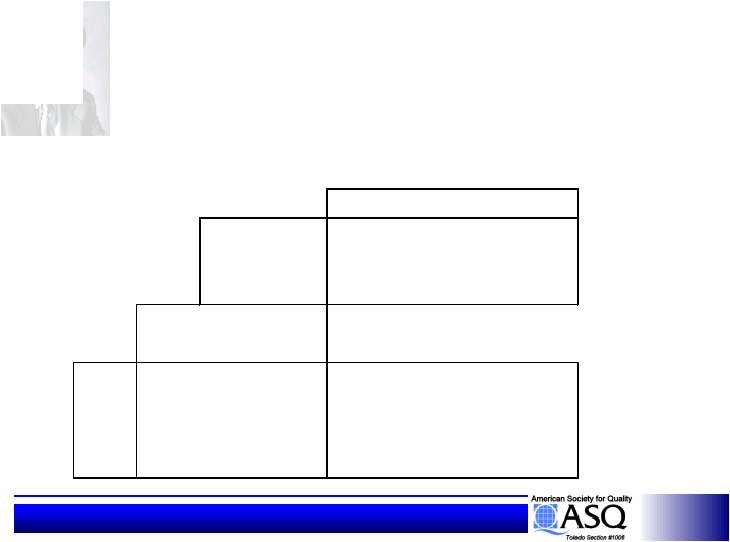Statistical Design of Experiments Statistical Design of Experiments Control Factors Control Factors A A B B C C (Inner Array) (Inner Array) Noise Factors Noise Factors L L M M N N (Outer Array) (Outer Array) 1 2 3 4 L 1 1 1 2 2 M 2 1 2 1 2 N 3 1 2 2 1 A B C 1 2 3 1 1 1 1 2 1 2 2 3 2 1 2 4 2 2 1 Results 15       17        10        12 15       17        10        12 18       20        13        17 18       20        13        17 18       15        14        13 18       15        14        13 23       16        19        15 23       16        19        15

Statistical Design of Experiments Statistical Design of Experiments Gold Plating Experiment Gold Plating Experiment System: System: Gold plating process Gold plating process Output response: Output response: y y - - Plating thickness ( Plating thickness ( m) m) Minimum specification: Minimum specification: 50 50 m m = 76 = 76 m m = 7.5 = 7.5 y Current Condition Current Condition

Statistical Design of Experiments Statistical Design of Experiments Noise Factor Noise Factor Level 1 Level 1 Level 2 Level 2 N: N: Part Location Part Location in plating tank in plating tank Off-center Off-center Center Center A: A: Gold Concentration Gold Concentration 0.70-0.75 0.70-0.75 1.10-1.15 1.10-1.15 Control Factors Control Factors Level 1 Level 1 Level 2 Level 2 Level 3 Level 3 B: B: Current Density Current Density 2.0 2.0 1.5 1.5 1.0 1.0 C: C: Temperature Temperature 95 95 105 105 115 115 D: D: Barrel Speed Barrel Speed 10 10 15 15 20 20 E: E: Anode Size Anode Size 1/4 1/4 1/2 1/2 1/1 1/1 F: F: Load Size Load Size 1/4 1/4 1/3 1/3 1/2 1/2 G: G: pH pH 4.20 4.20 4.30 4.30 4.40 4.40 H: H: Nickel Concentration Nickel Concentration 600 600 650 650 700 700

Statistical Design of Experiments Statistical Design of Experiments L 18 A B C D E F G H 1 1 1 1 1 1 1 1 1 83 88 90 91 27.9 88.00 2 1 1 2 2 2 2 2 2 73 73 83 81 23.4 77.50 3 1 1 3 3 3 3 3 3 57 58 65 69 20.7 62.25 4 1 2 1 1 2 2 3 3 55 59 61 67 21.6 60.50 5 1 2 2 2 3 3 1 1 73 75 76 79 29.6 75.75 6 1 2 3 3 1 1 2 2 58 60 68 72 19.8 64.50 7 1 3 1 2 1 3 2 3 44 49 55 58 18.3 51.50 8 1 3 2 3 2 1 3 1 50 54 57 64 19.6 56.25 9 1 3 3 1 3 2 1 2 64 65 66 68 31.7 65.75 10 2 1 1 3 3 2 2 1 74 79 86 94 19.6 82.25 11 2 1 2 1 1 3 3 2 75 78 90 94 19.2 84.50 12 2 1 3 2 2 1 1 3 70 76 85 88 19.7 79.75 13 2 2 1 2 3 1 3 2 71 80 87 95 18.2 83.25 14 2 2 2 3 1 2 1 3 48 56 59 65 18.1 57.00 15 2 2 3 1 2 3 2 1 66 67 79 86 17.7 74.50 16 2 3 1 3 2 3 1 2 45 53 58 64 17 2 3 2 1 3 1 2 3 60 67 66 73 18 2 3 3 2 1 2 3 1 57 65 79 83 Note: Two Readings were measured on each plated part N1 N2 y

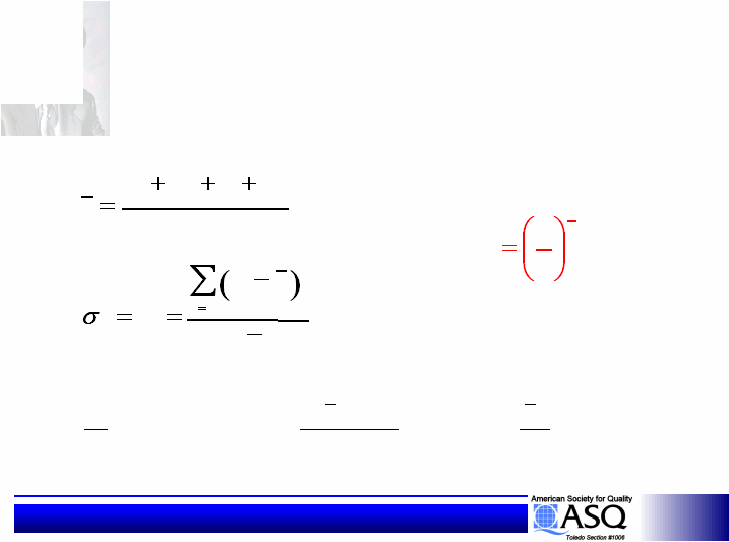Statistical Design of Experiments Statistical Design of Experiments S/N Ratio Concept S/N Ratio Concept n n y Around Mea y Around Mea Variabilit Variabilit an an Effect of Me Effect of Me N N S S S/N Ratio Calculation Note: For x dB gain in S/N, initial x opt Range RANGE * 2 1 6 . n y y y y n ... 2 1 n 1 1 2 2 n y y V i i e (dB ) ( ) ( ) ÷ ÷ ø ö ç ç è æ = ú û ù ê ë é - = = 2 2 2 log * 10 log * 10 s h y V n V y n N S e e For n data: y For n data: y 1 1 y y 2 2 y y 3 3 …y …y n n

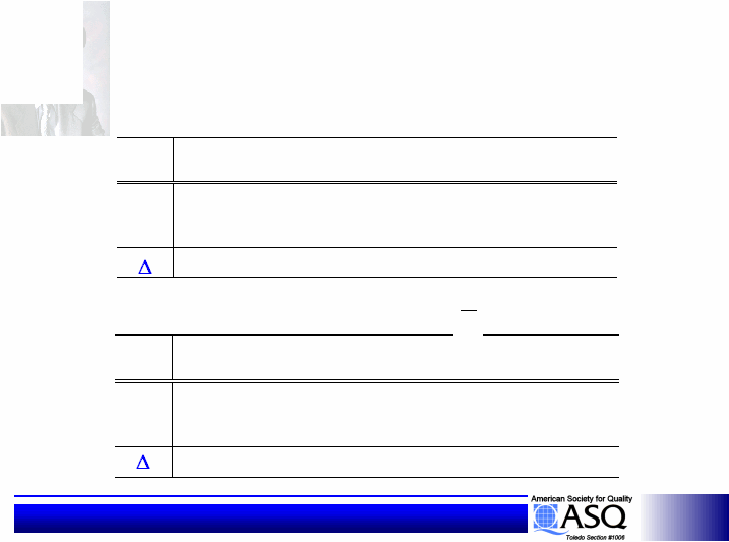Statistical Design of Experiments Statistical Design of Experiments Response Tables Response Tables A B C D E F G H 1 21.7 20.4 23.3 19.7 21.2 21.6 2 20.8 21.9 20.7 19.8 21.6 21.4 3 20.6 20.8 19.1 23.6 20.3 20.1 1.1 1.5 4.2 3.9 1.3 1.5 * in (dB) Factor Response Table (S/N)* Level Response Table Level Factor A B C D E F G H 1 66.9 70.3 73.3 73.0 70.2 74.8 2 72.8 69.6 73.1 69.2 69.6 71.8 3 69.6 63.0 67.3 69.6 62.9 5.9 0.7 4.2 5.7 0.6 11.9 y

Statistical Design of Experiments Statistical Design of Experiments Two Step Optimization Two Step Optimization 1. 1. Reduce Variability (maximize S/N) Reduce Variability (maximize S/N) 2. 2. Adjust mean to target Adjust mean to target A B C D E F G H Factor Factor Affect Affect S/N S/N Affect Affect Affect Affect S/N S/N Affect Affect S/N &     S/N &     Affect Affect Affect Affect Neither Neither y y y

Statistical Design of Experiments Statistical Design of Experiments E1 E1 1 E2 E2 2 23- 22- 21- 20- 19- 18- T E3 E3 3 Prediction - Prediction - Using Additivity Using Additivity A1 A1 1 A2 A2 2 23- 22- 21- 20- 19- 18- T D1 D1 1 D2 D2 2 23- 22- 21- 20- 19- 18- T D3 D3 3 G1 G1 1 G G 2 2 G3 G3 3 23- 22- 21- 20- 19- 18- T Prediction Equation Prediction Equation T G T E T D T A T opt = 1 3 1 1 ˆ = 21.0+(23.6-21.0)+(23.3-21.0)+(23.6-21.0)+(23.9-21.0) = 21.0+(23.6-21.0)+(23.3-21.0)+(23.6-21.0)+(23.9-21.0) +(23.6-21.0)+(23.3-21.0)+(23.6-21.0)+(23.9-21.0) (23.6-21.0)+(23.3-21.0)+(23.6-21.0)+(23.9-21.0) -21.0)+(23.3-21.0)+(23.6-21.0)+(23.9-21.0) 21.0)+(23.3-21.0)+(23.6-21.0)+(23.9-21.0) +(23.3-21.0)+(23.6-21.0)+(23.9-21.0) (23.3-21.0)+(23.6-21.0)+(23.9-21.0) -21.0)+(23.6-21.0)+(23.9-21.0) 21.0)+(23.6-21.0)+(23.9-21.0) +(23.6-21.0)+(23.9-21.0) (23.6-21.0)+(23.9-21.0) -21.0)+(23.9-21.0) 21.0)+(23.9-21.0) +(23.9-21.0) (23.9-21.0) -21.0) 21.0) = 31.4 dB = 31.4 dB Suppose the initial design was A Suppose the initial design was A 2 2 B B 2 2 C C 2 2 D D 2 2 E E 2 2 F F 2 2 G G 2 2 H H 2 2 T G T E T D T A T initial = 2 2 2 2 ˆ = 21.0+(18.5-21.0)+(20.7-21.0)+(19.8-21.0)+(20.1-21.0) = 21.0+(18.5-21.0)+(20.7-21.0)+(19.8-21.0)+(20.1-21.0) = 16.1 dB = 16.1 dB

Statistical Design of Experiments Statistical Design of Experiments Confirmation Run Confirmation Run Conduct conformation runs for the initial Conduct conformation runs for the initial and the optimum designs and the optimum designs Calculate the S/N ratios for both designs, Calculate the S/N ratios for both designs, and compare to the predicted S/N ratios: and compare to the predicted S/N ratios: S/N Prediction Confirmation Variable Data Initial Design 16.1 dB Optimum Design 31.4 dB Gain 15.3 dB Once the S/N ratio is confirmed (variability Once the S/N ratio is confirmed (variability reduction confirmed), observe the mean of reduction confirmed), observe the mean of the confirmation run, then adjust it to target. the confirmation run, then adjust it to target. 20.1 dB 20.1 dB 31.9 dB 31.9 dB 11.8 dB 11.8 dB 5 . 7 , 76 1 n y 2 . 2 , 87 1 n y