Articles

Sampling inspection is commonly used in quality to evaluate products and services. However, looking only at a part of the full selection introduces risks, as conclusions apply to the entire amount. This is where Operating Characteristic (OC) curve become handy.

They provide a clear way to study and better design sampling plans.

OC curves visually map how well a sampling method separates good from flawed batches. It shows the chances a lot passes testing at different quality levels, usually as a % of defects.

In other words, it demonstrates how capable the sampling setup is to differentiate between high and low-standard lots.

Factors like sample sizes, acceptance guidelines, and defect distributions determine an OC’s shape and position.

By examining these curves, quality pros can assess risks in passing or failing lots. They optimize sampling to make informed quality calls and production oversight decisions.

Overall, OC curves uphold sampling use by objectively verifying method proficiency. Their clarity empowers continuous assessment and upgrading of approaches over time.

Key Highlights

• Operating Characteristic (OC) curve provide a clear picture of how well sampling separates good batches from flawed ones.
• The graphs map the chances a lot passes testing (y-axis) against the quality level (x-axis), usually shown as a % of defects. This visual shows sampling performance distinguishing high vs low standard lots.
• OC curves play an important role in acceptance sampling, quality monitoring, and statistical process control. They are useful tools for examining how effective sampling methods are.
• They help identify the right sample sizes, passing guidelines, and risks in approving or failing lots based on quality targets.
• OC curves aid in balancing producer versus customer risks while optimizing inspection costs. They ensure products meet the quality standards set.
• These curves support informed choices. Their clarity fosters balanced, cost-effective approaches upholding quality over the long run. Continuous re-evaluation helps sampling fulfill its role in assurance.

What is the Operating Characteristic (OC) Curve?

The Operating Characteristic (OC) curve is a helpful statistical tool in quality control and acceptance sampling.

It provides a clear picture showing the relationship between the chances a lot passes testing and the actual quality level.

Sampling to assess if batches meet standards is common in manufacturing, supply chains, and quality systems. OC curves play a fundamental role in understanding how well this works.

The graphs help answer important questions like:

• The probability of high quality lots are approved?
• The probability of poor-quality ones are rejected?
• How does the plan perform at different levels?

Quality teams can examine a sampling method’s ability to differentiate the great and poor batches by studying the OC curve.

This insight is important when deciding to accept or reject shipments, as well as making sampling better at achieving desired standards and balanced risks.

OC curves simply map testing passing chances on the y-axis against the percentage of defects on the x-axis. Their position and shape deliver valuable clues about performance in various scenarios.

These visualizations provide objective perspectives supporting informed management of quality acceptance approaches.

Understanding the Operating Characteristic Curve (OC Curve)

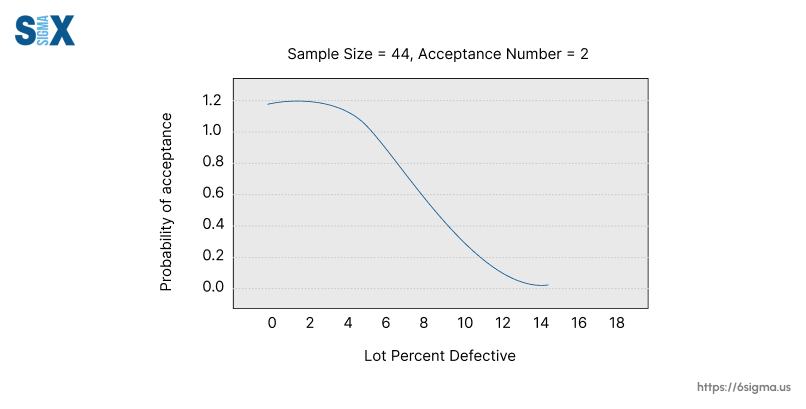
The operating characteristic (OC) curve is a graphical representation that depicts the probability of accepting or rejecting a lot based on the sampling plan and the quality level of the product or process. It is a fundamental tool in acceptance sampling and quality control.

The OC curve plots the probability of acceptance on the y-axis against the quality level or percent defective on the x-axis.

The quality level represents the fraction or percentage of defective items in the lot or process output.

The shape of the OC curve provides valuable insights into the performance of the sampling plan.

An ideal OC curve has a sharp, vertical drop from a high probability of acceptance to a low probability near the acceptable quality level (AQL). This indicates that the sampling plan can effectively discriminate between good and bad quality lots.

There are two important points on the Operating Characteristic curve:

1. Producer’s Risk (α): This is the probability of rejecting a lot when the quality level is equal to or better than the AQL. It is represented by the point where the OC curve intersects the acceptable quality level line.
2. Consumer’s Risk (β): This is the probability of accepting a lot when the quality level is equal to or worse than the rejectable quality level (RQL). It is represented by the point where the OC curve intersects the rejectable quality level line.

The OC curve helps balance the risks between the producer (supplier) and the consumer (customer). A good sampling plan aims to minimize both the producer’s and consumer’s risks while keeping the sample size and inspection costs reasonable.

Constructing the Operating Characteristic Curve (OC Curve)

The operating characteristic (OC) curve is a graphical representation that displays the probability of accepting a lot as the percent defective or nonconforming units increase.

Constructing an accurate OC curve is essential for the proper implementation of acceptance sampling plans.

Determining Sample Size and Acceptance Number

The first step is determining the appropriate sample size and acceptance number for the sampling plan being used (single, double, multiple, etc).

The sample size (n) is the number of units selected from the lot for inspection. The acceptance number (c) is the maximum allowable number of defective units in the sample. These are chosen based on the desired producer’s risk (α) and consumer’s risk (β) levels.

Calculating Probabilities 

Once n and c are set, the probability of acceptance Pa(p) can be calculated for various levels of percent defective (p) using the appropriate probability distribution model:

• Binomial distribution for attribute sampling 
• Poisson distribution for narrow limits on percent defective
• Hypergeometric distribution for variables sampling

This gives a set of coordinates (p, Pa(p)) that can be plotted to form the OC curve.

Plotting the Operating Characteristic Curve

The x-axis represents the percent defective or nonconforming units (p). The y-axis represents the probability of acceptance Pa(p).

By plotting the calculated probability points, a smooth OC curve can be drawn connecting the points.

The curve will have an S-shape, with Pa(p) approaching the producer’s risk α as p approaches 0, and Pa(p) approaching the consumer’s risk β as p increases.

Interpreting the Curve

The shape and position of the OC curve convey important information about the discriminatory power of the sampling plan between good and bad lots.

Ideally, the curve should have a relatively steep slope transitioning from the producer’s risk to the consumer’s risk over a narrow range of percent defective values.

This allows reasonably good discrimination between acceptable and unacceptable quality levels.

Sampling Plans and Operating Characteristic Curve

The operating characteristic (OC) curve is closely tied to the sampling plan used for inspection. Different sampling plans will produce different OC curves. The three main types of sampling plans are:

Single Sampling Plan

In a single sampling plan, a single random sample of n units is taken from the lot and inspected. The number of defective units (d) in the sample is counted.

If d is less than or equal to an acceptance number c, the entire lot is accepted. Otherwise, it is rejected.

The single sampling plan is defined by the sample size n and acceptance number c. The OC curve shows the probability of acceptance for different levels of percent defective in the lot.

Double Sampling Plan

A double sampling plan involves two potential samples. An initial sample of n1 units is taken. If the number of defects d1 is less than or equal to an acceptance number c1, the lot is accepted. If d1 is greater than a rejection number r1, the lot is rejected. Otherwise, a second sample of n2 units is taken.

The total number of defects d1 + d2 is then compared to an acceptance number c2. If it is less than or equal to c2, the lot is accepted, otherwise it is rejected.

The double sampling plan requires more parameters: n1, c1, r1, n2, c2. The OC curve shows the probability of acceptance for different quality levels.

Multiple Sampling Plan

A multiple-sampling plan extends the double-sampling concept to allow for more than two samples before deciding on lot acceptance or rejection. It provides additional discrimination for borderline cases.

The OC curve is used to evaluate the discriminatory power and other characteristics of these different sampling plans for a given situation. Appropriate sampling plans can be selected by studying their OC curves.

Lot Formation and Sampling Justification

Before constructing an operating characteristic (OC) curve or implementing a sampling plan, it is crucial to properly define and form the inspection lot.

An inspection lot refers to the group of units or products that will be evaluated through acceptance sampling.

Proper lot formation ensures that the sample taken is representative of the entire batch or production run.

There are several factors to consider when defining an inspection lot:

Homogeneity – The units within the lot should be relatively homogeneous in terms of materials, manufacturing process, and expected quality level. This ensures the sample provides an accurate depiction.

Traceability – The lot should be identifiable and traceable back to specific operations, machines, raw materials, etc. This aids in troubleshooting if quality issues arise.

Size – The lot size should strike a balance between being too large (difficult to control) or too small (inefficient sampling). Established guidelines often recommend lot sizes.

Once the lot is formed, the appropriate sampling plan must be determined based on the acceptable quality level (AQL), inspection process capabilities, and the risks associated with acceptance/rejection.

The sample size is a critical factor that directly impacts the operating characteristic curve. A larger sample size reduces the risks of incorrect acceptance/rejection but increases inspection costs.

Established sampling plans like MIL-STD-105E guide sample sizes for different lot sizes and AQLs.

The acceptance number, which specifies how many defective units are allowed for a sample to be accepted, is another key parameter.

It is determined based on the producer’s and consumer’s risks of making an incorrect decision.

Justifying the sampling approach is important to balance quality risks with operational costs and efficiencies.

Factors like the criticality of the product, manufacturing process controls, supplier quality history, and consequences of acceptance/rejection errors are all considered.

Applications and Case Studies of Operating Characteristic Curve

The operating characteristic (OC) curve has wide applications across various industries for quality control and process monitoring purposes. Some common examples include:

Manufacturing

OC curves are extensively used in manufacturing to determine acceptable quality levels (AQLs) and sampling plans for inspecting incoming raw materials or outgoing finished products.

This helps ensure products meet customer specifications while minimizing inspection costs.

For example, an automotive company may use an OC curve to set up a sampling plan to inspect a percentage of engines from each production lot.

The curve allows them to calculate the probability of accepting good-quality lots and rejecting poor ones.

Food Safety

OC curves play a vital role in food safety by aiding in microbiological testing and inspections.

They help determine sample sizes and acceptance criteria for factors like bacterial counts to protect consumers.

A meat processing plant could use an OC curve to create a Hazard Analysis and Critical Control Points (HACCP) sampling plan to test for pathogens like Salmonella.

The curve guides decisions on acceptance of lots based on calculated producer’s and consumer’s risks.

Healthcare 

The healthcare industry uses OC curves for sampling inspection of medical devices, pharmaceuticals, and clinical trials.

These curves ensure products are safe and effective before reaching patients.

For instance, a medical device manufacturer may apply an OC curve to set up acceptance sampling of pacemaker batteries based on AQL, sample size, and probability of approval.

The curve informs decisions that balance product quality with inspection costs.

Service Industries

Though less common, OC curves can also benefit service industries like call centers, where managers may use these curves to monitor service quality through attributes like call resolution rates.

A software company could employ an OC curve to sample and inspect a portion of software releases for bug detection before product launch, minimizing risks to customers.

These examples highlight how OC curves facilitate data-driven decision-making for quality management across diverse sectors, optimizing processes while controlling risks and costs.

Advantages, Limitations, and Best Practices

Advantages of Operating Characteristic (OC) Curve

• OC curves provide a visual representation of the performance of a sampling plan, allowing for easy interpretation and comparison of different plans.
• They quantify the producer’s risk (alpha) and consumer’s risk (beta) associated with a sampling plan.
• OC curves account for the quality level or percent defective of the lot being sampled.
• They can be used to select an appropriate sampling plan that balances producer’s and consumer’s risks.
• OC curves help determine the sample size needed to meet desired performance criteria.

Limitations of OC Curves  

• Constructing OC curves requires knowledge of the underlying distribution (binomial, hypergeometric, Poisson) and associated parameters.
• The OC curve is specific to the sampling plan used; a new curve must be generated for different sampling plans.
• For very small sample sizes, the discrete nature of the OC curve may be difficult to interpret visually.
• OC curves assume stable process conditions; they do not account for process shifts or drifts over time.
• Applying OC curves requires an understanding of statistical concepts like acceptable quality level (AQL).

Best Practices for Using Operating Characteristic (OC) Curve

• Clearly define the product/process requirements and associated AQL before selecting a sampling plan.
• Consider both producer’s and consumer’s risks when choosing an OC curve and sampling plan.
• For attribute sampling, use the appropriate statistical distribution (binomial, hypergeometric, Poisson) when generating the OC curve.
• Complement OC curve analysis with other quality control tools like control charts for process monitoring.
• Periodically review sampling plans and update OC curves if process conditions change significantly.
• Provide training to ensure proper interpretation and application of OC curves by quality professionals.
• Use statistical software or online calculators to simplify the generation of OC curves.

By understanding the advantages, limitations, and best practices, manufacturers can effectively leverage operating characteristic curve as a valuable tool in acceptance sampling and quality control.